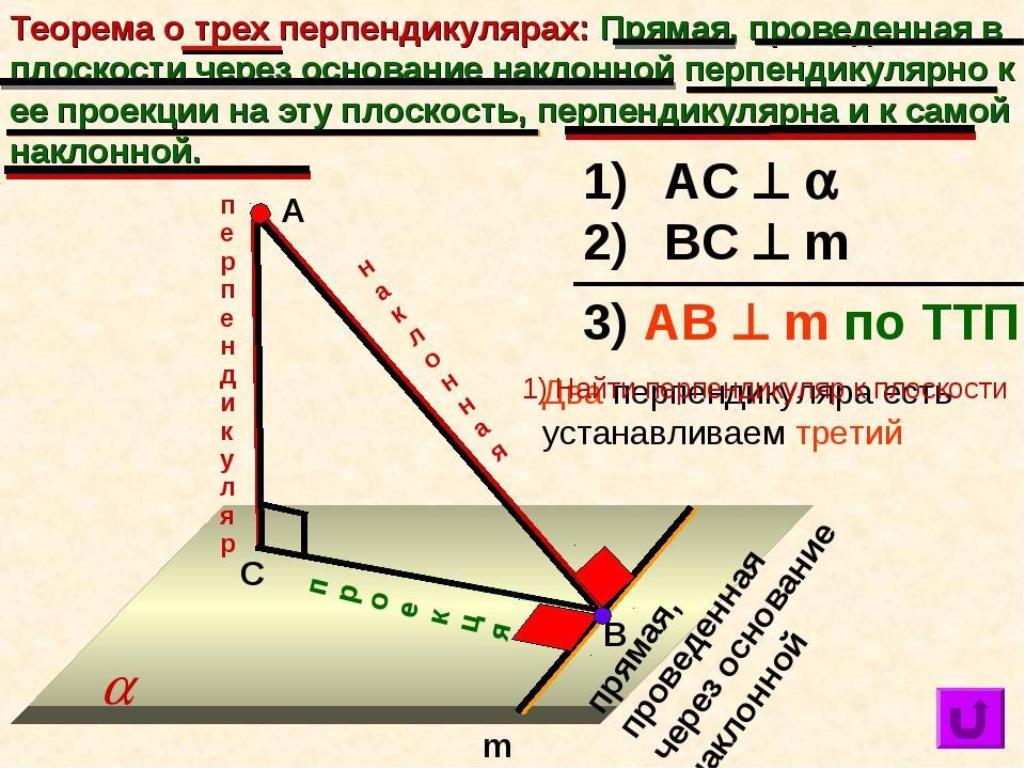
Теорема о перпендикуляре: Как правильно провести перпендикуляр из точки к прямой и доказать его уникальность

Теорема о перпендикуляре является одной из основополагающих в геометрии и в математике в целом. Понимание этой теоремы необходимо не только для изучения геометрии, но и для применения в различных областях, включая физику, архитектуру и даже инвестиции. В этой статье мы рассмотрим, как правильно провести перпендикуляр из точки к прямой, а также докажем его уникальность.

Определение перпендикуляра

Перпендикуляр — это линия, которая образует угол в 90 градусов с другой линией или плоскостью. В контексте нашей темы, мы будем говорить о перпендикуляре, проведенном из точки к прямой.

Условия для проведения перпендикуляра

Для того чтобы провести перпендикуляр из точки к прямой, должны быть выполнены следующие условия:

Наличие прямой, к которой нужно провести перпендикуляр.
Наличие точки, из которой будет проведен перпендикуляр.

Пошаговая инструкция по проведению перпендикуляра

Процесс проведения перпендикуляра из точки к прямой можно разбить на несколько шагов:

Выберите прямую, к которой будете проводить перпендикуляр.
Определите точку, из которой будете проводить перпендикуляр.
Используя линейку и угломер, отметьте точку пересечения перпендикуляра с прямой.
Проведите линию, соединяющую исходную точку и точку пересечения.

Доказательство уникальности перпендикуляра

Теперь перейдем к доказательству уникальности перпендикуляра. Ранее мы отметили, что из одной точки можно провести только один перпендикуляр к данной прямой. Доказательство этого утверждения можно провести следующим образом:

Предположения

Пусть у нас есть прямая \( l \) и точка \( A \), которая не лежит на этой прямой. Мы будем доказывать, что существует только одна прямая, проходящая через точку \( A \) и перпендикулярная прямой \( l \).

Доказательство

Проведем перпендикуляр \( AP \) из точки \( A \) к прямой \( l \), где \( P \) — точка пересечения.
Предположим, что существует другая прямая \( AQ \), которая также перпендикулярна \( l \) и проходит через точку \( A \).
Так как угол между перпендикуляром и прямой всегда равен 90 градусов, это означает, что угол \( APQ \) также равен 90 градусов.
Однако, угол не может одновременно быть 90 градусов для двух различных линий, проходящих через одну и ту же точку и пересекающих одну и ту же прямую.
Следовательно, \( AP \) и \( AQ \) должны совпадать, что доказывает уникальность перпендикуляра из точки к прямой.

Примеры проведения перпендикуляра

Для лучшего понимания, приведем несколько примеров:

Пример	Описание
Пример 1	Проведение перпендикуляра из точки над прямой.
Пример 2	Проведение перпендикуляра из точки под прямой.
Пример 3	Проведение перпендикуляра из точки на одной линии с прямой.

Заключение

Теорема о перпендикуляре — это не только фундаментальный аспект геометрии, но и важный инструмент в различных практических применениях. Понимание того, как правильно провести перпендикуляр и доказать его уникальность, является важной частью математического образования. Надеемся, что данная статья помогла вам разобраться в этом вопросе и даст возможность применять знания на практике.

Вопросы и ответы

Вопрос	Ответ
Что такое теорема о перпендикуляре?	Теорема о перпендикуляре утверждает, что из любой точки, не лежащей на прямой, можно провести единственный перпендикуляр к этой прямой.
Как провести перпендикуляр из точки к прямой?	Для проведения перпендикуляра необходимо использовать циркуль и линейку: вывести окружность с центром в данной точке, найти точки пересечения с прямой и провести прямую через центр и одну из точек пересечения.
Почему перпендикуляр из точки к прямой уникален?	Уникальность перпендикуляра доказывается тем, что если бы существовал другой перпендикуляр, то он бы пересекал первый в одной и той же точке, что противоречит определению перпендикуляра.
Какие инструменты нужны для доказательства теоремы о перпендикуляре?	Для доказательства теоремы о перпендикуляре обычно используются линейка, циркуль и метод доказательства от противного.
Каковы практические приложения теоремы о перпендикуляре?	Теорема о перпендикуляре находит применение в архитектуре, инженерии и геометрическом черчении, где важно точно определять углы и расстояния.